반응형
동전 i(1≤i≤n)개를 쓰며, j(0≤j≤10) 원을 만드는 모든 경우에 대해 DP를 수행해주면 된다.
예제 입력1에 대해 표를 만들어 보았다.
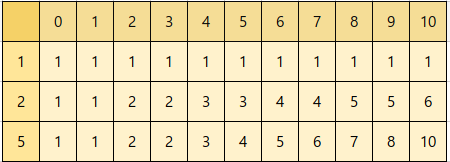
먼저, 1원 동전으로 0원부터 10원을 만드는 경우의 수는 모두 1이다.
2원 동전으로 0,1원을 만들 수는 없으므로 갱신하지 않고 그대로 1을 따라간다.
2원 동전으로 2원 이상을 만들 때부턴 새로운 경우가 발생한다.
1,2원 동전으로 j-2원을 만드는 경우의 수를 현재 값에 더해주면 되는데,
1,2원 동전으로 j-2원을 만드는 경우들에 2원 동전 하나만 더 추가하면 j원이 완성되기 때문에 이 경우들을 추가해주는 것이다.
1,2,5원 동전을 모두 사용하는 경우에도 똑같이 이를 적용해보자.
5원 동전으로는 5원 이상을 만들 때부터 새로운 경우가 발생한다.
1,2,5원 동전으로 j-5원을 만드는 경우의 수를 현재 값에 더해주면 된다.
똑같은 이유로 이 경우들에 5원 동전 하나만 더 추가하면 j원이 완성되기 때문에 이 경우를 더해주는 것이다.
이 원리로 DP를 수행하면 어렵지 않게 답을 찾을 수 있다.
위의 표는 갱신과정을 보여주기 위해 2차원 표로 나타낸 것이고
실제 DP는 1차원 배열로 수행한다.
#include <iostream>
#include <queue>
#include <vector>
#include <algorithm>
#include <string>
#include <string.h>
#include <stack>
using namespace std;
int dp[10001];
int input[101];
int main() {
int n,k;
cin >> n >> k;
for(int i=1;i<n+1;i++){
cin >> input[i];
}
dp[0] = 1;
for(int i=1;i<n+1;i++){
for(int j=1; j<k+1;j++){
if(j-input[i] >= 0) dp[j] += dp[j-input[i]];
}
}
cout << dp[k];
}반응형
'Algorithm > Dynamic' 카테고리의 다른 글
| [동적계획법, 난이도 중] 백준 9251번 LCS (0) | 2020.09.01 |
|---|---|
| [동적계획법, 난이도 중] 백준 1699번 제곱수의 합 (0) | 2020.08.31 |
| [동적계획법, 난이도 중하] 백준 11057번 오르막 수 (0) | 2020.08.30 |
| [동적계획법, 난이도 중] 백준 11052번 카드 구매하기 (0) | 2020.08.28 |
| [동적 계획법, 난이도 중] 백준 9465번 스티커 (0) | 2020.08.27 |




댓글