두 수열의 부분수열을 찾는 문제이므로 2차원 DP방식을 이용하였다.
예제 입력 1에서 주어진 입력은
ACAYKP
CAPCAK 이다.
동적계획법을 이용하여 길이가 작은 문자열~긴 문자열들 순으로 수행해나가면 된다.
맨 처음, 2번째 문자열에서 길이가 1인 "C"를 1번째 문자열과 비교해 나갈 것이다.
A 와 C -> 0
AC 와 C -> 1
ACA 와 C -> 1
ACAY 와 C -> 1
ACAYK 와 C -> 1
ACAYKP 와 C -> 1
그 다음, 2번째 문자열에서 길이가 2인 "CA"를 1번째 문자열과 비교해 나갈 것이다.
A 와 CA -> 1
AC 와 CA -> 1
ACA 와 CA -> 2
ACAY 와 CA -> 2
ACAYK 와 CA -> 2
ACAYKP 와 CA -> 2
이 순서로 수행해 나간다면 맨 마지막에는 ACAYKP, CAPCAK을 비교하게 될 것이다.
갱신 규칙은 이렇다.
문자열1의 일부와 문자열2의 일부를 각각 한 문자씩 비교해나가다가 같은 문자가 나왔다는 것은, 비교중인 각 일부 문자열들 길이보다 각각 1씩 작은 문자열들의 최장 공통 부분 수열의 길이에 1이 늘어났다는 의미가 되는 것이다.
예를 들어, ACA와 CAPCA를 비교중이라고 가정해보자.
여기서 신경 써야 될 것은 끝문자가 모두 A로 같다는 것이다.
이 문자열들 길이보다 1씩 작은 문자열은 각각 AC, CAPC 이고 이들의 최장 공통 부분 수열의 길이는 2인데,
이 문자열들의 끝에 같은 문자(A) 가 추가 된 것이 현재 비교중인 문자열들이기 때문에
최장 공통 부분 수열의 길이는 2에 1을 더한 3이 되는 것이다.
그렇다면 끝문자가 다를 경우에는 어떨까?
ACAY와 CAPC를 비교중이라고 가정해보자.
여기서 신경 써야 될 것은 끝 문자가 Y와 C로 다르다는 것이다.
이들의 최장 공통 부분 수열의 길이는
ACAY와 CAP의 최장 공통 부분 수열길이와 같을 수도 있고,
ACA와 CAPC의 최장 공통 부분 수열길이와 같을 수도 있다.
즉, 이 둘중 최댓값을 ACAY와 CAPC의 최장 공통 부분 수열길이로 정하면 되는 것이다.
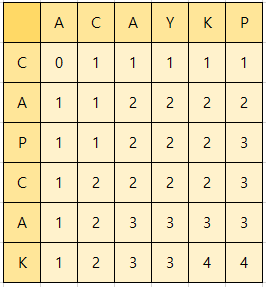
이 과정을 표로 완성해보면 이렇다.
#include <iostream>
#include <queue>
#include <vector>
#include <algorithm>
#include <string>
#include <string.h>
#include <math.h>
#include <stack>
using namespace std;
int ans[1002][1002];
int maxi(int a, int b) {
if(a > b) return a;
else return b;
}
int main() {
string s1;
string s2;
cin >> s1 >> s2;
int size1 = s1.size();
int size2 = s2.size();
for (int i = 1; i < size2 + 1; i++) {
for (int j = 1; j < size1 + 1; j++) {
if (s2[i - 1] == s1[j - 1]) {
ans[i][j] = ans[i - 1][j - 1]+1;
}
else ans[i][j] = maxi(ans[i - 1][j], ans[i][j - 1]);
}
}
cout << ans[size2][size1];
}
'Algorithm > Dynamic' 카테고리의 다른 글
| [동적계획법, 난이도 중하] 프로그래머즈, 등굣길 (0) | 2020.09.28 |
|---|---|
| [동적계획법, 난이도 중상] 프로그래머즈, 도둑질 (0) | 2020.09.08 |
| [동적계획법, 난이도 중] 백준 1699번 제곱수의 합 (0) | 2020.08.31 |
| [동적계획법, 난이도 중] 백준 2293번 동전 1 (0) | 2020.08.30 |
| [동적계획법, 난이도 중하] 백준 11057번 오르막 수 (0) | 2020.08.30 |




댓글