입력이 단순히 일렬로 주어지지 않고, 2차원 표 형식으로 주어지는 종류의 DP문제다.
스티커를 인접하지 않게 고를 수 있는 최대 점수를 계산하는 문제다.
그래도 이 문제는 O(N) 의 시간 복잡도로 해결 할 수 있다. 스티커가 2행 n열로 배치되어 있는데 1열당 2개의 스티커씩 n회 만큼만 DP를 수행하면 된다.
이런 유형의 DP는 한 열 단위로 DP를 수행하려고 하지말고 각 열의 1행, 2행에 대한 DP를 모두 수행해야 한다.
이 문제에서 주어진 예제로 DP를 수행하는 원리를 설명한다.
진행은 1열부터 n열 순으로한다.
입력값
| 50 | 10 | 100 | 20 | 40 |
| 30 | 50 | 70 | 10 | 60 |
두 인접한 스티커는 같이 고를 수 없으므로 초기값은 1열의 값 그대로다.

이제 2열은 위에서 부터 스티커 점수가 10, 50인데, (30+10=40), (50+50=100) 처럼 스티커를 대각선으로 골라야 서로 인접하지 않는 스티커들의 최대 점수합이 된다.

그러나 3열부터는 꼭 인접한 대각선에 있는 스티커만 골라야 하는 것이 아니다.
200은 50+50+100 의 조합, 즉 최대 스티커수로 만들 수 있지만
120은 (30+10+70=110), (50+70=120) 둘중 최댓값인 50과 70의 조합의 합으로 만들어진 값이다.
스티커를 무조건 많이 붙일 수록 최댓값이 나오는 것이 아니라는 의미다.

즉 최댓값은 인접한 대각선에 있는 DP값에 현재 자리의 스티커를 고르거나,
인접한 대각선에서 한칸 더 떨어진 DP값에 현재 자리의 스티커를 고르는 경우 둘 중 하나가 된다.
아래사진은 후자의 경우이다.
(첫 번째 칸 ...은 이전까지 수행한 DP)

물론 세 열이나 떨어진 경우는 고려할 필요가 없다.
흐린 X 자리에도 얼마든지 스티커를 붙일 수 있기 때문이다.
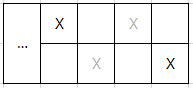
이렇게 두 가지 경우중 점수가 최대가 되는 경우를 골라 DP를 계산해 나가면 최종적으론 이렇게 된다.

마지막 열의 250, 260 중 최댓값인 260이 이 문제의 답이 된다.
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <math.h>
using namespace std;
int maxi(int a, int b) {
if (a > b) return a;
else return b;
}
int input[100001][2];
int vec[100001][2];
int main() {
int t;
cin >> t;
for (int i = 0; i < t; i++) {
int row;
cin >> row;
for (int j = 1; j < row + 1; j++) {
cin >> input[j][0];
}
for (int j = 1; j < row + 1; j++) {
cin >> input[j][1];
}
vec[1][0] = input[1][0];
vec[1][1] = input[1][1];
for (int j = 2; j < row + 1; j++) {
vec[j][0] = maxi(vec[j - 2][1], vec[j - 1][1])+input[j][0];
vec[j][1] = maxi(vec[j - 2][0], vec[j - 1][0])+input[j][1];
}
cout << maxi(vec[row][0], vec[row][1]) << endl;
}
}
+2021-10-15 백준 숏코딩 상위 1% C++
#include <iostream>
#include <algorithm>
using namespace std;
int d[100001][2];
int n,T;
int main()
{
cin>>T;
for(int t=0;t<T;t++){
cin>>n;
for(int i=1;i<=n;i++)cin>>d[i][0];
for(int i=1;i<=n;i++)cin>>d[i][1];
for(int i=2;i<=n;i++){
d[i][0]=max(d[i-1][1],d[i-2][1])+d[i][0];
d[i][1]=max(d[i-1][0],d[i-2][0])+d[i][1];
}
cout<<max(d[n][0],d[n][1])<<"\n";
}
}'Algorithm > Dynamic' 카테고리의 다른 글
| [동적계획법, 난이도 중하] 백준 11057번 오르막 수 (0) | 2020.08.30 |
|---|---|
| [동적계획법, 난이도 중] 백준 11052번 카드 구매하기 (0) | 2020.08.28 |
| [동적계획법, 난이도 중] 백준 14501번 퇴사 (0) | 2020.08.26 |
| [동적계획법, 난이도 중] 백준 9461번 파도반 수열 (0) | 2020.08.25 |
| [동적계획법, 난이도 중] 백준 11053번 가장 긴 증가하는 부분 수열 (0) | 2020.08.24 |




댓글