반응형
DP는 점화식은 짧지만 생각이 결론에 도달하여 점화식을 만드는데까지는 시간이 다소 오래 걸린다는 특징이 있다.
특히 이런 도형문제가 그런 편인 것 같은데, 도형쪽으로 센스가 있다면 쉽게 풀 수 있을 것이다.
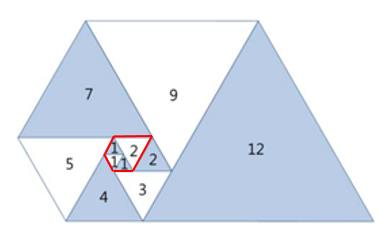
기준이 되는 첫 삼각형은 크기가 1인 정삼각형이라고 했는데, 아래에 빨간 테두리로 쳐 둔 정삼각형이 기준인 것 같다.
그래야 시계 방향으로 자연스럽고 보기좋게 갱신이 가능하다.

여기서 잘 보면 4번째 삼각형을 처음 포함했을 때부터 쭉 오각형 형태가 유지되며, 6번째 삼각형을 포함하게 될 때부터 새롭게 포함되는 삼각형은 2개의 삼각형 변과 인접하게 된다.
그 2개의 삼각형은 i를 현재 포함하려는 삼각형이라고 하면, i-5번째 삼각형과 i-1번째 삼각형에 해당된다.
이해를 돕기 위해 아래 그림을 첨부하였다.
 |
 |
 |
 |
 |
즉, DP는 5번째 삼각형(i=5일때, save[i-5]=0) 또는 6번째 삼각형부터 시작하면 되고,
점화식은 save[i]=save[i-5]+save[i-1] 로 세울 수 있다.
#include <iostream>
using namespace std;
long long save[101];
int test[101];
int main() {
int n;
cin >> n;
for (int i = 1; i < n + 1; i++) {
cin >> test[i];
}
save[1] = 1;
save[2] = 1;
save[3] = 1;
save[4] = 2;
save[5] = 2;
for (int i = 6; i < 101; i++) {
save[i] = save[i - 5] + save[i - 1];
}
for (int i = 1; i < n + 1; i++) {
cout << save[test[i]] << endl;
}
}반응형
'Algorithm > Dynamic' 카테고리의 다른 글
| [동적 계획법, 난이도 중] 백준 9465번 스티커 (0) | 2020.08.27 |
|---|---|
| [동적계획법, 난이도 중] 백준 14501번 퇴사 (0) | 2020.08.26 |
| [동적계획법, 난이도 중] 백준 11053번 가장 긴 증가하는 부분 수열 (0) | 2020.08.24 |
| [동적계획법, 난이도 중] 백준 10844번 쉬운 계단 수 (0) | 2020.08.20 |
| [동적계획법, 난이도 중상] 백준 1912번 연속합 (0) | 2020.08.19 |




댓글