반응형
문제를 해결한 후에도 다른 풀이법에 대한 호기심이 생겨서 찾아보았다.
내 풀이법도 간단하다고 생각하지만 이 블로그에 설명된 풀이법이 더 간단해보이니 궁금한 분들은 참고하길 바란다. https://hwan-shell.tistory.com/308
이제 내 풀이법을 소개한다.
해결 방법
cookie 벡터에 대한 누적합 배열 cookie_acc을 만들어 놓았기 때문에 구간합 공식을 쉽게 구할 수 있었다. 예를 들어, 구간 [a, b]에 대한 구간합은 cookie_acc[b]-cookie_acc[a-1]이다.
이 문제에서는 a<b를 만족하는 모든 구간 [a, b]을 확인하여, 과자의 수를 정확히 반으로 나눌 수 있는 m값이 존재하는 경우들에 대한 cookie_acc[b]-cookie_acc[m]값의 최댓값을 구하면 된다.
구간합의 1/2이 지금까지 계산한 한 명의 아들에게 줄 수 있는 과자수의 최댓값보다 작다면 해당 구간은 확인할 필요도 없으니 다음 반복문을 수행(continue)하면 된다(11줄 참고). 그리고 각 구간에서 m값은 최대 하나만 존재할 수 있기 때문에, m을 찾았다면 로직을 수행하고 반복문을 빠져나가(break)줘야 연산을 줄일 수 있다.
소스 코드
#include <vector>
using namespace std;
int answer, cookie_acc[2001];
int solution(vector<int> cookie) {
// 누적 cookie 계산
for(int i=0;i<cookie.size();i++) cookie_acc[i]=cookie_acc[i-1]+cookie[i];
for(int a=0;a<cookie.size();a++){
for(int b=a+1;b<cookie.size();b++){
if((cookie_acc[b]-cookie_acc[a-1])/2<answer) continue;
for(int m=a;m<b;m++){
if(cookie_acc[m]-cookie_acc[a-1]==cookie_acc[b]-cookie_acc[m]){
answer=max(answer, cookie_acc[b]-cookie_acc[m]);
break;
}
}
}
}
return answer;
}
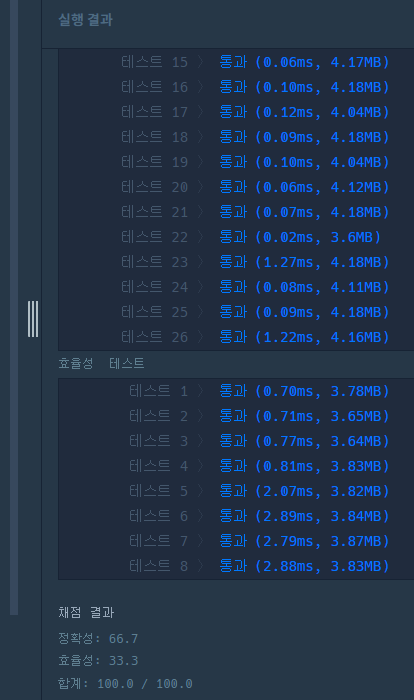
테스트케이스 정확성, 효율성 모두 만점
반응형
'Algorithm > 기타 알고리즘' 카테고리의 다른 글
| [Linked List] 표 편집 - 2021 카카오 채용연계형 인턴십 (0) | 2022.05.22 |
|---|---|
| [시뮬레이션] 수식 최대화 - 2020 카카오 인턴십 (0) | 2022.05.14 |
| [시뮬레이션] 스킬트리 - Summer/Winter Coding(~2018) (0) | 2022.04.29 |
| [수학] 멀쩡한 사각형 - Summer/Winter Coding(2019) (0) | 2022.04.22 |
| [시뮬레이션] 행렬 테두리 회전하기 - 2021 Dev-Matching (0) | 2022.03.27 |




댓글