반응형
해결 방법
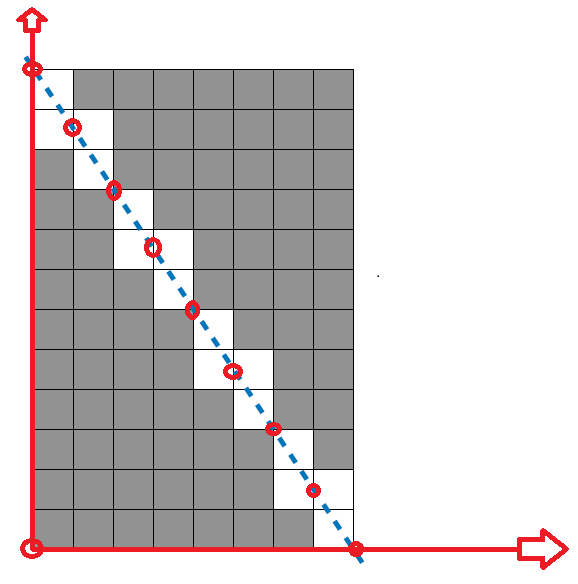
일차 함수의 특성을 이용하여 문제를 해결했다.
입출력 예 #1에서 좌측 하단 꼭짓점을 원점이라고 했을 때, 일차 함수식은 다음과 같다.
y=-(h/w)x+h
x축으로 좌표를 1씩 옮겨가며 선에 걸치는 사각형들을 제거해주는 방법을 사용하면 문제를 해결할 수 있다.
이제, 좌측에 있는 사각형부터 제거해보자.
먼저 x=0일 때 y=12이고, x=1일 때 y=10.5다. 이 경우에는 y의 좌표가 10~12 사이에 있는 사각형 2개가 제거된다.

그 다음에 x=1일 때 y=10.5이고, x=2일 때 y=9다. 이 경우에는 y의 좌표가 9~11 사이에 있는 사각형 2개가 제거된다.

이런식으로 계속 두 좌표를 비교하여 사각형을 제거해나가면 되는데, 이 때 왼쪽 좌표의 y값은 올림을 하고 오른쪽 좌표의 y값은 내림을 한 후 두 정수의 차이를 구했음을 알 수 있다.
(0, 12)와 (1, 10.5)를 비교했을 때는 12-10=2개의 사각형이 제거된 것이고,
(1, 10.5)와 (2, 9)를 비교했을 때는 11-9=2개의 사각형이 제거된 것이다.
또, w, h의 입력 범위가 1억까지이기 때문에 정수형은 long long으로, 실수형은 double로 지정했다.
자료형의 범위에 대해 잘 숙지하지 못했다면 이 문제를 풀기 힘들었을 것이다.
소스 코드
#include <cmath>
using namespace std;
long long solution(int w,int h) {
long long answer = (long long) w*h;
long long y1, y2;
for(int i=1;i<=w;i++){
y1=ceil((double)-1*h*(i-1)/w+h);
y2=floor((double)-1*h*i/w+h);
answer-=(long long)y1-y2;
}
return answer;
}
테스트케이스 18개 모두 통과

반응형
'Algorithm > 기타 알고리즘' 카테고리의 다른 글
| [구간합] 쿠키 구입 - Summer/Winter Coding(~2018) (0) | 2022.05.01 |
|---|---|
| [시뮬레이션] 스킬트리 - Summer/Winter Coding(~2018) (0) | 2022.04.29 |
| [시뮬레이션] 행렬 테두리 회전하기 - 2021 Dev-Matching (0) | 2022.03.27 |
| [투 포인터] 보석 쇼핑 - 2020 카카오 인턴십 (0) | 2022.03.20 |
| [시뮬레이션] 오픈채팅장 - 2019 카카오 블라인드 채용 (0) | 2022.03.05 |




댓글