반응형
백준 11053번 가장 긴 증가하는 수열 문제를 응용한 문제이다.
[동적계획법, 난이도 중] 백준 11053번 가장 긴 증가하는 부분 수열
제한 시간은 1초며, N의 범위가 (1 ≤ N ≤ 1,000) 으로 좁은 편이기 때문에 O(N^2) 까지 쓸 수 있다. 그래도 이 문제는 1차원 배열의 DP로 풀 수 있다. 첫 INPUT에 대한 DP의 첫 인덱스 값을 1로 두며 시작��
kimcoder.tistory.com
가장 긴 증가하는 수열을 정방향, 역방향 2번 계산하여 해결할 수 있는데
계산 과정은 위 포스팅에 자세히 설명해놨으므로 이 포스팅에선 설명을 따로 하지 않을 것이다.
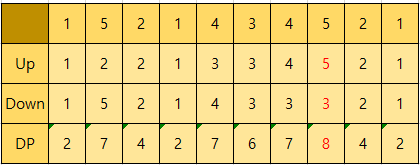
아래에 예제 입력1 계산표에서
Up행은 가장 긴 증가하는 수열을 적용한 DP이고,
Down행은 가장 긴 감소하는 수열을 적용한 DP이다. 가장 긴 증가하는 수열을 마지막 인덱스부터 거꾸로 적용했다는 의미도 되겠다.
해당 행의 두 요소를 합한 값에 1을 뺀(겹치는 경우) 값이 이 문제의 최종 DP값이 되고, DP값은 현재 요소가 꼭대기값일 때의 바이토닉 수열 길이가 된다. 바이토닉 수열은 한번 올라갔다 내려간 한 세트의 수열이라서, 최대로 올라간 값을 꼭대기값이라고 하였다.
<예제 입력1 계산표>
#include <iostream>
#include <queue>
#include <vector>
#include <algorithm>
#include <string>
#include <string.h>
#include <stack>
using namespace std;
int save[1001]; //부분증가수열
int save2[1001]; //부분감소수열
int newsave[1001];
int input[1001];
int maxi(int a1,int b1) { return (a1>b1)? a1:b1; }
int mini(int a2,int b2) { return (a2<b2)? a2:b2; }
int main() {
int n;
cin >> n;
int ans=0;
for (int i = 1; i < n + 1; i++) {
cin >> input[i];
}
save[1] = 1;
save2[n] = 1;
for (int i = 2; i < n + 1; i++) {
int max = 0;
int max2 = 0;
for (int j = 1; j < i; j++) {
if ((input[j] < input[i])&&(save[j]>max)) {
max = save[j];
}
if ((input[n-j+1] < input[n-i+1])&&(save2[n-j+1]>max2)) {
max2 = save2[n-j+1];
}
}
if (max == 0) save[i] = 1;
else save[i] = max +1;
if (max2 == 0 ) save2[n-i+1] = 1;
else save2[n-i+1] = max2 + 1;
}
for(int i=1;i<n+1;i++){
newsave[i] = save[i]+save2[i];
ans = maxi(ans,newsave[i]);
}
cout << ans-1;
}반응형
'Algorithm > Dynamic' 카테고리의 다른 글
| [동적계획법] 스티커 모으기(2) - Summer/Winter Coding(~2018) (0) | 2022.04.12 |
|---|---|
| 동적계획법 고득점 kit 풀이 완료, 후기 (0) | 2020.09.28 |
| [동적계획법, 난이도 중하] 프로그래머즈, 등굣길 (0) | 2020.09.28 |
| [동적계획법, 난이도 중상] 프로그래머즈, 도둑질 (0) | 2020.09.08 |
| [동적계획법, 난이도 중] 백준 9251번 LCS (0) | 2020.09.01 |




댓글