n개의 연결된 루프에 매댈 수 있는 최대 무게를 구할 수 있어야 한다.
이 문제의 예제는 부실하므로 버틸 수 있는 최대 중량이 각각 7, 15, 30, 11, 5인 루프 5개를 준비하였다.
일단 이 루프를 내림차순으로 정렬했다.
30, 15, 11, 5, 7
먼저 최대 중량이 30인 밧줄은 당연히 중량이 30인 물체까지 버틸 수 있다.

그렇다면 1,2번째로 최대 중량이 높은 밧줄인 30, 15를 묶으면 어디까지 버틸 수 있을까?
k개의 루프가 묶인다면 중량은 k분의 1로 나뉘게 된다고 했다.
2번째로 최대 중량이 높은 15에 2를 곱한 30이 최대가 된다.
중량이 30인 물체는 저 밧줄들에 각각 15, 15씩 분배가 되므로 30이 최대가 된다는 것을 검산했다.

그렇다면 1,2,3번째로 최대 중량이 높은 밧줄인 30, 15, 11을 묶으면 어디까지 버틸 수 있을까?
3번째로 최대 중량이 높은 11에 3을 곱한 33이 최대가 된다.
중량이 33인 물체는 저 밧줄들에 각각 11, 11, 11씩 분배가 되므로 33이 최대가 된다는 것을 검산했다.
즉, n개의 줄을 묶었을 때 n번 줄의 최대중량에 n을 곱한 값이 최대로 들어올릴 수 있는 중량이 된다.

똑같이 아래 케이스에선 저 밧줄 4개를 묶었을 때 무게가 7x4=28 인 물체까지 버틸 수 있고,
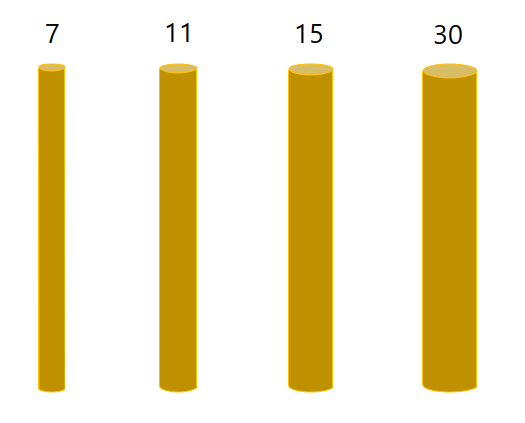
이 케이스에선 밧줄 5개를 모두 묶었을 때 무게가 5x5=25 인 물체까지 버틸 수 있다.

지금까지 5개의 경우를 종합해보면 밧줄 11, 15, 30을 묶었을 때 중량이 최대 33인 물체까지 버틸 수 있다는 사실을 알 수 있다.
이 접근법을 소스코드로 옮기면 이렇다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int rope[100001];
int gd[100001];
int main() {
int n;
cin >> n;
for (int i = 1; i < n + 1; i++) {
cin >> rope[i];
}
sort(rope+1, rope + n + 1, greater<int>());
int max = 0;
for (int i = 1; i < n + 1; i++) {
gd[i] = rope[i]*i;
if (gd[i] > max) max = gd[i];
}
cout << max;
}'Algorithm > Greedy' 카테고리의 다른 글
| [그리디, 난이도 중] 프로그래머즈, 섬 연결하기 (0) | 2020.09.30 |
|---|---|
| [그리디, 난이도 중하] 프로그래머즈, 체육복 (0) | 2020.09.12 |
| [그리디, 난이도 중] 프로그래머즈, 단속카메라 (0) | 2020.09.10 |
| [그리디, 난이도 중] 백준 1543번 문서 검색 (0) | 2020.08.17 |
| [그리디, 난이도 중] 백준 1931번 회의실배정 (0) | 2020.08.14 |




댓글