반응형
해결 방법
필자는 DFS와 BFS를 기반으로 완전탐색을 이용해서 해결했다. BFS를 통해 현재 커서로부터 각 칸까지 이동할 때 필요한 최소 키 조작 횟수를 구했다. 예를 들어, 입출력 예 #1에서 최초로 실행되는 BFS 결과는 다음과 같다. 1칸 이동, 일괄 이동의 경우를 모두 반영했다.
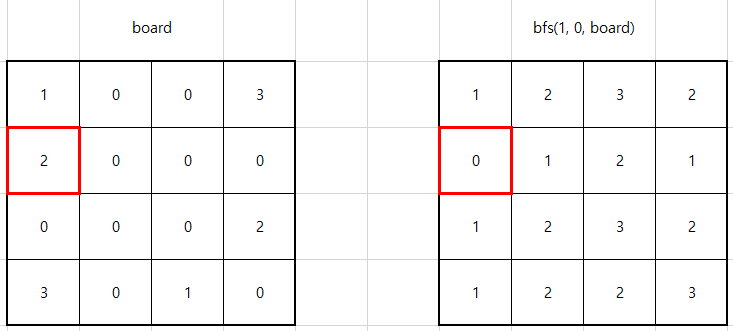
그리고 DFS에서는 뒤집혀 있는 카드의 상태에 따라 동작 방식이 다르다. 소스 코드에서는 뒤집혀 있는 카드의 상태를 state 변수에 저장했다. state가 0인 경우에는 어떠한 카드도 뒤집혀 있지 않은 상태고, state가 0이 아닌 경우에는 뒤집혀 있는 카드의 번호가 저장되어 있다.
DFS는 다음과 같이 동작한다.
- state==0 : 현재 뒤집힌 카드가 없다면 남아있는 모든 카드를 한 번씩은 뒤집어본다.
- state!=0 : 뒤집힌 카드의 짝 카드를 찾아서 뒤집는다.
카드를 뒤집을 때는 board의 해당 칸의 값을 0으로 지정해주면서 남은 카드의 수도 카운트다운 하면 된다. 하나의 dfs 탐색이 끝났다면 다음 dfs 탐색에 영향을 주지 않도록 이전 상태로 복구시켜야 한다.
소스 코드
#include <queue>
#include <vector>
using namespace std;
int answer=-1;
int lx[4]={0, 0, 1, -1};
int ly[4]={1, -1, 0, 0};
struct Point {int x; int y; int step;};
vector<vector<int>> bfs(int x, int y, vector<vector<int>> board) {
vector<vector<int>> min_step(4, vector<int>(4, -1));
min_step[x][y]=0; // 커서가 있는 칸은 0으로 초기화
queue<Point> q; // 갱신된 칸에 대한 정보를 큐에 삽입
q.push({x, y, 0});
while(!q.empty()) {
Point fp = q.front();
q.pop();
int nx, ny;
for(int k=0;k<4;k++) { // 1칸 이동의 경우
nx=fp.x+lx[k]; ny=fp.y+ly[k];
if(nx<0||nx>=4||ny<0||ny>=4) continue;
if(min_step[nx][ny]==-1) {
min_step[nx][ny]=fp.step+1;
q.push({nx, ny, min_step[nx][ny]});
}
}
for(int k=0;k<4;k++) { // 일괄 이동의 경우
nx=fp.x; ny=fp.y;
while(1) { // 조건에 맞을 때까지 nx 또는 ny를 이동
if(nx+lx[k]<0||nx+lx[k]>=4||ny+ly[k]<0||ny+ly[k]>=4) break;
nx+=lx[k]; ny+=ly[k];
if(board[nx][ny]!=0) break;
}
if(min_step[nx][ny]==-1) {
min_step[nx][ny]=fp.step+1;
q.push({nx, ny, min_step[nx][ny]});
}
}
}
return min_step;
}
void dfs(int x, int y, int state, int step, vector<vector<int>> board, int cnt) {
if(cnt==0) { // 남은 카드가 없는 경우
if(answer==-1) answer=step;
else answer=min(answer, step);
return;
}
vector<vector<int>> min_step = bfs(x, y, board); // 키 조작 횟수 벡터 반환
int temp;
for(int i=0;i<4;i++) {
for(int j=0;j<4;j++) {
// 현재 뒤집힌 카드가 없다면 남아있는 모든 카드를 한 번씩은 뒤집어보고, 뒤집힌 카드가 있다면 짝 카드를 찾아서 뒤집는다.
if(state==0?board[i][j]!=0:board[i][j]==state) {
temp=board[i][j];
board[i][j]=0;
dfs(i, j, state==0?temp:0, step+min_step[i][j]+1, board, cnt-1);
board[i][j]=temp;
}
}
}
}
int solution(vector<vector<int>> board, int r, int c) {
int cnt=0; // 남은 카드의 개수
for(int i=0;i<4;i++) for(int j=0;j<4;j++) if(board[i][j]!=0) cnt++;
dfs(r, c, 0, 0, board, cnt);
return answer;
}
테스트케이스 30개 모두 정답
문제 출처 : https://school.programmers.co.kr/learn/courses/30/lessons/72415
반응형
'Algorithm > Brute force' 카테고리의 다른 글
| [완전탐색] 양궁대회 - 2022 KAKAO BLIND RECRUITMENT (0) | 2022.10.18 |
|---|---|
| [완전탐색] 메뉴 리뉴얼 - 2021 KAKAO BLIND RECRUITMENT (1) | 2022.09.23 |
| [완전탐색] 외벽 점검 - 2020 KAKAO BLIND RECRUITMENT (0) | 2022.09.08 |
| [완전탐색] 후보키 - 2019 KAKAO BLIND RECRUITMENT (0) | 2022.06.24 |
| 완전탐색 고득점 kit 풀이 완료, 후기 (0) | 2020.09.24 |




댓글