1. 함수적 종속
1) 함수적 종속이란?
- 어떤 릴레이션에서 X와 Y를 각각 속성의 부분집합이라고 할 때, X의 값을 알면 Y의 값을 바로 식별할 수 있고, X의 값에 Y의 값이 달라질 때, Y는 X에 함수적 종속이라고 한다. 이 경우 X를 결정자, Y를 종속자라고 하고 기호로 표현하면 X→Y이다. 또는 Attribute 단위로 표현하기 위해 X1 X2 ... Xn → Y1 Y2 ... Ym으로 표현해도 된다.
- 하나의 FD f(부분집합)에 대하여 어떠한 인스턴스든 함수적 종속을 만족한다면, 릴레이션은 함수적 종속을 만족한다고 할 수 있다.
예시 1 - (title, year) 쌍이 나머지 Attribute들을 결정하는 경우 -> 함수적 종속 만족

예시 2 - (title, year) 쌍이 나머지 Attribute들을 결정하지 않는 경우 -> 함수적 종속 불만족
(title, year, starName)이 결정자(key)가 돼야 함수적 종속을 만족함

2) 릴레이션 속성의 부분집합 X가 key가 되기 위한 조건
- X는 릴레이션의 모든 다른 속성들을 함수적으로 결정해야 함 (모든 속성을 포함하는 closure 집합)
- X의 진부분집합(⊂ 또는 ⊃)이 없어야 함 : 최소한의 속성으로 이루어져야 함
3) Superkey
- key의 superset
- key를 포함하는 집합 : 모든 key는 superkey가 될 수 있고, superkey는 진부분집합을 허용함
4) 함수적 종속의 추론
- 어떠한 함수적 종속을 통하여 다른 함수적 종속도 추론할 수 있다는 개념
※ 예) Transitive rule : 릴레이션 R(A, B, C)에서 A->B이고 B->C라면, A->C가 성립된다.
- S가 T에 따른다면, T에 있는 모든 함수적 종속을 만족하는 모든 인스턴스는 S에 있는 모든 함수적 종속을 만족한다.
※ 예) {A->C}는 {A->B, B->C}에 따른다.
- 두 FD 집합 S와 T가 동일하다면, S를 만족하는 인스턴스 집합과 T를 만족하는 인스턴스 집합은 같고, S과 T는 서로를 따른다.
2. 함수적 종속의 규칙
[어떤 릴레이션에서 A, B, C를 속성의 부분집합이라고 가정]
1) The splitting/combining rule
A->B1, A->B2, ... A->Bm으로 쪼개어서 표현할 수도 있고, A->B1 B2... Bm으로 통합하여 표현할 수도 있다는 규칙
2) Trivial 함수적 종속
- B가 A의 부분집합이라면 A1 A2 ... An -> B1 B2 ... Bm이 성립한다는 규칙
※ 예) title year -> title
- C의 속성들이 A의 속성들이 아닌 B의 속성들과 동일하더라도 A->B는 A->C와 같다.
※ 좌항에도 존재하는 우항의 속성은 제거할 수 있음
예제 - 릴레이션 R(A, B, C, D, E, F)에서 FD 집합 S{AB->C, BC->AD, D->E, CF->B}

※ 원래의 FD 요소들은 손실시키지 말것
3) Closure of attributes
- S를 FD의 집합이라고 했을 때, S에 있는 모든 FD들을 만족하는 릴레이션 B에 대하여 A->B를 만족한다면 B는 A의 closure에 해당된다.
- A에 의해 함수적으로 결정되는 모든 attribute들의 집합을 A의 closure이라고 한다.
- closure 추가 절차 : closure 집합 X에 모든 A를 담아두고, B가 X의 부분 집합이면서 B->C를 만족하면 C를 X에 추가하는 작업을 더 이상 X에 추가할 attribute들이 없을 때 까지 진행
- A의 closure 범위가 릴레이션의 모든 attribute들을 포함하면서 진부분집합이 존재하지 않는다면 A는 key가 될 수 있다. (어떤 진부분 집합에 대한 closure 범위가 릴레이션의 모든 attribute들을 포함하면 안된다는 뜻)
- closure을 통해 A->B가 FD의 집합 S를 따르는지 확인할 수 있다. A의 closure 집합을 계산해서, B가 closure 집합에 포함된다면 A->B는 S를 따른다고 판단할 수 있다.

예제 1 - closure 집합 구하기

답 : C={title, year, length, genre, studioName}
예제2 - 릴레이션 R(A, B, C, D, E, F)에서 FD 집합 S{AB->C, BC->AD, D->E, CF->B}
(문제 1) {A, B}+의 추가 과정 : {A, B} >> {A, B, C} >> {A, B, C, D} >> {A, B, C, D, E}
{A, B}+ : {A, B, C, D, E}
(문제 2) AB->D가 S에 따름을 증명
AB의 closure 집합은 D를 포함한다.
(문제 3) D->A가 S에 따르는지 확인
D의 closure 집합은 {D, E}로 A를 포함하지 않으므로, S에 따르지 않는다.
4) Transitive rule
A->B이고 B->C라면, A->C가 성립한다.
5) Armstrong's axioms(암스트롱의 공리)
- Reflexivity : B⊆A라면, A->B가 성립한다.
- Augmentation(증가) : A->B라면, AC->BC가 성립한다.
- Transivity : A->B이고 B->C라면, A->C가 성립한다.
예제

3. 관계형 데이터베이스 설계
1) Anomaly(모순)
(1) 의미
- 데이터의 삽입, 삭제, 수정 시 발생하는 중복, 무결성 저하, 논리적 오류 현상
예시 1

- Movies(title, year, length, genre, studioName, starName, gender)
- title year -> length genre studioName
- key = {title, year, starName}
문제 유발 요소들
- length, genre 값은 여러 튜플들에서 중복적으로 나타날 수 있음
- 부분적 종속 발생 : title year -> length genre studioName, starName -> gender
- Update anomaly : 하나의 튜플에 있는 정보만 변경되고, 나머지 동일 정보는 변경되지 않았을 때 발생함
※ 예) 1번째 튜플에 있는 "Star Wars, 1977"의 길이만 변경
- Deletion anomaly : 하나의 튜플이 삭제되었을 때 다른 attribute들에 있는 정보들도 잃을 수도 있음
※ 예) Vivian Leigh 튜플을 삭제했을 때 Gone With the Wind 영화에 대한 모든 정보가 사라질 수 있음
※ 예) Gone With the Wind 튜플을 삭제했을 때 Vivian Leigh 배우에 대한 모든 정보가 사라질 수 있음
예시 2 - Movies, MoviesStudio에 대한 attribute들을 같이 사용할 때

- Movies(title, year, length, genre, studioName, starName, gender)
- title year -> length genre studioName
- key = {title, year, starName}
문제 유발 요소들
- Insertion Anomaly : key가 null인 튜플들을 삽입할 수 없음
※ 예) 새 studio가 생성되었지만 key {title, year}가 null이기 때문에 테이블에 삽입할 수 없음
- Deletion anomaly : 예) studio에 하나의 영화만 존재하는 경우, 그 영화 정보를 삭제하면 studio에 있는 정보들까지 잃을 수 있다.
2) Decomposing(분해) Relations
(1) 분해의 법칙
- 릴레이션을 분해하여 Anomaly들을 제거할 수 있음(모순의 제거)
- 릴레이션 A를 분해해서 릴레이션 B, C를 생성했다면, A=BUC가 성립해야 하고, 결합했을 때에도 정보가 잘 복구 되어야 함(정보의 복구)
※ 예) (title, year, length, genre, studioName, starName)를 key{title, year} 기준으로 분해하면 (title, year, length, genre, studioName), (title, year, starName)로 나뉜다.
- 분해/결합 시 모든 FD(함수적 종속성)들은 보존되어야 한다(종속성의 보존). 그렇지 않으면 결합시 중복이 발생할 수 있음
(2) 분해로 인해 발생할 수 있는 모순
- 두 릴레이션을 결합했을 때 spurious(가짜) 튜플들이 발생할 수 있음
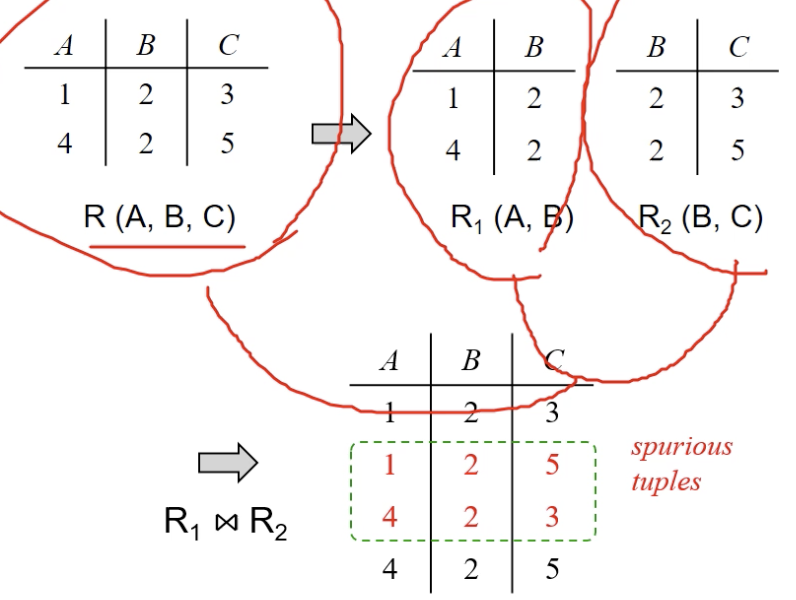
- BCNF를 만족하는 형태로 분해했더라도, 다시 결합했을 때 함수적 종속들이 보존되지 않는 경우가 있을 수 있음. 이 때에는 3NF을 만족하는 형태로 분해해야 함
(3) Lossless join 분해
- 분해를 했더라도 특정 attribute에 대하여 projection을 했을 때 결과가 동일한 분해
- Lossless join 분해 판별법 : 릴레이션 R을 분해한 R1과 R2에 대하여, R1∩R2->R1 혹은 R1∩R2->R2인 경우
※ 예) R={A,B,C}, FD={A->B}, R1={A,B}, R2={A,C}일 때 A->AB가 성립함
(4) 3NF이 좋을까? BCNF가 좋을까?
- 3NF은 INSERTION, UPDATE, DELETION 모순의 제거가 이루어지지 않을 수 있음
- BCNF는 종속성의 보존이 이루어지지 않을 수 있음
- 목적에 따라서 결정해야 하는데, 3NF이 더 중요함
3) Boyce-Codd 정규화(BCNF)란?
- 릴레이션 R이 BCNF 상태에 있는 기준 : A->B에서 B가 A의 부분집합이 아니고(non-trivial), A가 R의 superkey인 경우
예시 1 - R(A, B)은 항상 BCNF 상태이다.
- nontrivial FD가 없는 경우 : BCNF
- A->B이 참이고, B->A은 거짓일 경우 : A가 key이기 때문에 BCNF
- A->B, B->A 모두 참일 경우 : A,B가 key이기 때문에 BCNF
예시 2 - R(title, year, length, genre, studioName, starName), FD: title year -> length genre studioName
length genre studioName가 title year의 부분집합은 아니지만, title year은 superkey가 아니기 때문에 BCNF 상태가 아님
부분적인 종속이 있고, 테이블에 값이 중복되는 attribute가 존재하기 때문에 중복이 발생할 수 있다.
예시 3 - R(title, year, length, genre, studioName), FD: title year -> length genre studioName
length genre studioName가 title year의 부분집합이 아니면서, title year은 superkey이기 때문에 BCNF 상태임
4) BCNF 정규화 과정
- Decomposition을 이용하면 됨
- 분해된 각 릴레이션은 BCNF 상태여야 하고, 기존 릴레이션은 분해된 릴레이션들에 의해 복원될 수 있어야 함
- Decomposition 과정 : nontrivial X->A에서 X가 R의 superkey가 아니라면, R1(X, A), R2=(R-A)로 분해한다. 이 과정을 더 이상 분해할 릴레이션이 없을 때까지 반복하면 된다.
예시 1 - R(title, year, length, genre, studioName, starName), FD: title year -> length genre studioName, Key: {title, year, starName}
nontrivial title year -> length genre studioName에서, title year은 superkey가 아니기 때문에 BCNF 상태가 아니다.
그래서 R1{title, year, length, genre, studioName}, R2{title, year, starName}으로 분해했다.
예시 2 - R(title, year, studioName, president, presAddr), FD: title year -> studioName, studioName -> president, president -> presAddr, Key: {title, year}
(Step 1) nontrivial title year -> studioName에서, title year은 superkey이기 때문에 BCNF 상태이다.
그러나 studioName -> president, president -> presAddr에 대해서는 BCNF 상태가 아니기 때문에 분해가 필요하다.
A->B, A->AB, B->C, A->C, AB->CB, A->BC
그래서 R1{studioName, president, presAddr}, R2{title, year, studioName}으로 분해했다.
(Step 2) R1의 FD: studioName -> president, president -> presAddr, Key: {studioName}
nontrivial studioName -> president에서, studioName은 superkey이기 때문에 BCNF 상태이다.
그러나 president -> presAddr에 대해서는 BCNF 상태이기 때문에 분해가 필요하다.
R1를 다시 분해하여 R3{president, presAddr}, R4{studioName, president}로 분해했다.
결과 : R2, R3, R4
5) Partial dependency(부분적 종속)
- X->A에서 X가 key의 진부분집합(⊂ 또는 ⊃)인 상태
- 중복성이 발생함
- 부분적 종속 관계를 완전한 종속 관계로 만드는 것을 2정규형(Second Normal Form)이라고 한다.
- 2정규형(2NF) : 1NF + nonprime attribute가 key에 완전히 종속적인 것(후보키 집합 K와 K에 속하지 않는 속성 A가 있을 때, A를 결정하기 위해 K의 일부가 아닌 K 전체를 참조해야만 하는 경우. 즉, 부분적 종속이 없는 경우)
※ 1NF : 모든 attribute들이 원자적인 하나의 값을 가지는 상태(attribute가 multivalued라면 일관성이 깨지는 문제가 발생할 수 있음)
※ nonprime attribute : key의 attribute가 아닌 attribute
6) Transitive dependency
- X->A에서 X가 어떠한 key의 진부분집합이 아닌 경우가 있음
- Decomposition으로 해결할 수 있음
- 3정규형(3NF) : 2NF + nonprime attribute가 transitive 종속을 가지지 않는 상태(즉 모두, 결정자가 superkey이거나 종속자의 속성들이 prime(key)인 경우)
- 3NF가 될 수 없는 경우 : transitive 종속성을 가지는 attribute가 존재

- 3NF가 되는 경우 : transitive 종속성을 가지는 attribute가 존재하지 않음


- 3NF 분해 과정 : 먼저, FD 집합에서 중복되거나 추론 가능한 FD를 제거한 minimal bases를 구한다. 그리고 각 X->A마다 XA스키마(X, A1, ... Am)를 생성한 뒤에 R2가 R1의 부분집합이라면 R2를 제거해나가는 과정을 반복한다. 만약 R의 key를 포함하는 스키마가 존재하지 않는다면 이 key를 구성하는 스키마를 추가한다.
예시 - R(A,B,C,D,E), F={AB->C, C->B, A->D}, keys:[{A,E,B}, {A,E,C}]
일단, AB, C, A는 모두 superkey가 아니다. 그리고 C와 B는 prime이지만 D는 prime이 아니기 때문에 A->D에 의해 3NF는 위배된다.
그리고 F의 minimal bases를 구해야 한다. 소거법을 이용하면 쉽게 구할 수 있다.
AB->C : AB->C를 제외한 {A,B}+가 C를 포함하는가? -> {A,B,D}이기 때문에 꼭 필요함
C->B : C->B를 제외한 {C}+가 B를 포함하는가? -> {C}이기 때문에 꼭 필요함
A->D : A->D를 제외한 {A}+가 D를 포함하는가? -> {A}이기 때문에 꼭 필요함
AB->C : A를 제외한 B->C : {B}+가 C를 포함하는가? -> {B}이기 때문에 꼭 필요함 (각 FD를 소거하는 과정)
AB->C : B를 제외한 A->C : {A}+가 C를 포함하는가? -> {A}이기 때문에 꼭 필요함
F는 이미 minimal basis 상태이기 때문에 바로 R1(A,B,C), R2(B,C), R3(A,D)로 쪼갤 수 있으며, R2는 R1의 부분집합이기 때문에 제거된다.
key를 포함하는 스키마가 존재하지 않으므로 {A,E,B} 또는 {A,E,C}를 추가하면 된다.
* 결과 : R1(A,B,C), R3(A,D), R4(A,B,E)
'DB > DB Concept' 카테고리의 다른 글
| SQL(2) - DDL (0) | 2022.01.30 |
|---|---|
| 제약 조건과 트리거 (0) | 2022.01.29 |
| SQL(1) - DML (1) | 2022.01.28 |
| Algebraic(대수) Query Language (0) | 2022.01.27 |
| E/R Model (0) | 2022.01.26 |




댓글